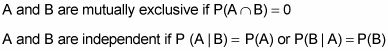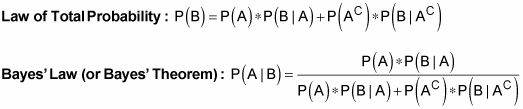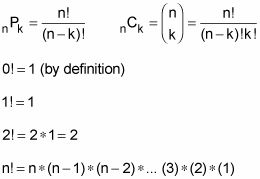El campo de las matemáticas de la probabilidad tiene sus reglas propias, definiciones y leyes, que se puede utilizar para encontrar la probabilidad de resultados, eventos o combinaciones de resultados y eventos. Para determinar la probabilidad, es necesario agregar o restar, multiplicar o dividir las probabilidades de los resultados y eventos originales. Usted utilizar algunas combinaciones tan a menudo que tienen sus propias reglas y fórmulas. Cuanto mejor conozca las ideas detrás de las fórmulas, lo más probable es que te acordarás de ellos y ser capaz de utilizar con éxito.
Reglas de probabilidad

Las definiciones de probabilidad
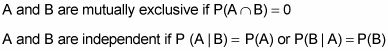
Leyes de probabilidad
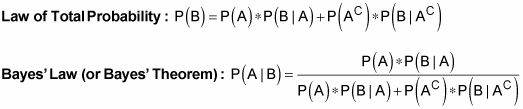
Contando reglas
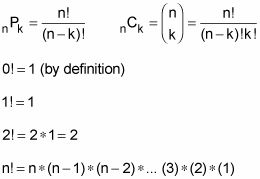
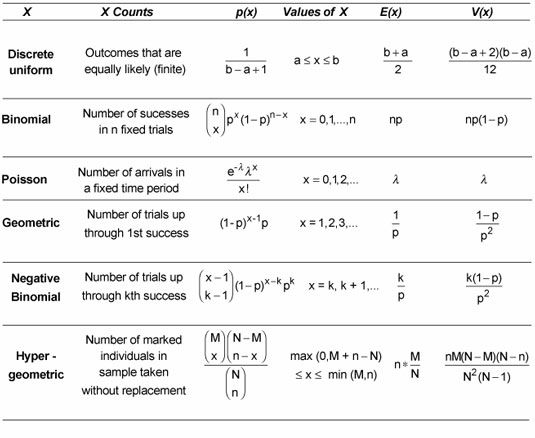
Distribuciones de probabilidad discretas
En probabilidad, una distribución discreta tiene ya sea un finito o un número infinito numerable de valores posibles. Eso significa que usted puede enumerar o hacer una lista de todos los valores posibles, tales como 1, 2, 3, 4, 5, 6 ó 1, 2, 3,. . .
Hay varios tipos de distribuciones de probabilidad discretas, incluyendo uniforme discreta, binomial, Poisson, geométrica, binomial negativa, y hipergeométrica.
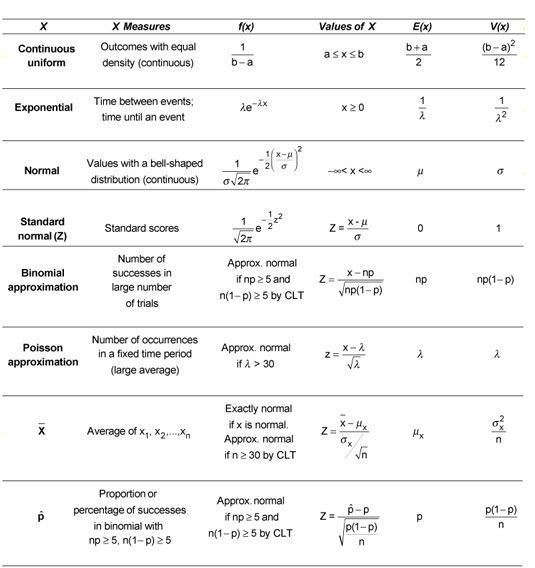
Distribuciones de probabilidad continuas
Cuando se trabaja con distribuciones de probabilidad continuas, las funciones pueden tomar muchas formas. Estos incluyen uniforme continua, exponencial, normal, normal estándar (Z), la aproximación binomial, Poisson aproximación, y distribuciones de la media muestral y la proporción de la muestra.
Cuando se trabaja con la distribución normal, es necesario tener en cuenta que se trata de un distribución continua, no uno discreto. Función de probabilidad de una distribución continua toma la forma de una curva continua, y su variable aleatoria lleva en un número infinito de posibles uncountably valores. Esto significa que el conjunto de valores posibles se escribe como un intervalo, tales como infinito negativo hasta el infinito positivo, cero a infinito, o un intervalo como [0, 10], que representa a todos los números reales entre 0 y 10, incluyendo 0 y 10.
Consejos de estudio de probabilidad
Si usted va a tomar un examen de la probabilidad, usted puede mejorar sus posibilidades de sobresalir en la prueba mediante el estudio de los siguientes temas. Tienen una alta probabilidad de estar en el examen.
La relación entre los eventos mutuamente excluyentes e independientes
Identificar cuando una probabilidad es una probabilidad condicional en un problema de palabras
Conceptos de probabilidad de que van en contra de la intuición
Probabilidades marginales, condicionales y conjuntas para una tabla de doble entrada
El teorema del límite central:
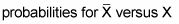
Cuándo utilizar una permutación y cuándo usar una combinación
Encontrar E (X) a partir de cero y su interpretación
El muestreo con reemplazo frente sin reemplazo
La ley de la probabilidad total y teorema de Bayes
Cuando la Poisson y exponencial se necesitan en el mismo problema