¿Cómo encontrar soluciones para una función de la trigonometría de múltiples ángulos
Funciones trigonométricas múltiples ángulos incluyen
etcétera. Al considerar las relaciones inversas (que dan respuestas múltiples) para estos ángulos, el multiplicador ayuda a determinar el número de respuestas a esperar. Usted toma el número de respuestas que se encuentra en una rotación completa y lo dejan a veces el multiplicador. Por ejemplo, si usted está buscando
en la ecuación
a continuación, se obtienen dos respuestas diferentes si se tiene en cuenta todos los ángulos entre 0 y 360 grados:
es igual a 60 y 120 grados. Pero si cambia la ecuación para
se obtiene el doble, o cuatro, respuestas entre 0 y 360 grados:
es igual a 30, 60, 210 y 240 grados. Estos ángulos se encuentran a una rotación, pero su puesta en la ecuación y multiplicación inicial da ángulos con el mismo lado del terminal como los ángulos dentro de una rotación.
Estos son algunos ejemplos para mostrar cómo funciona esta multiplicación y cómo encontrar las respuestas. En primer lugar, que le muestre cómo obtener las respuestas a
Escribe la ecuación inversa.
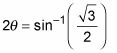
Lista de todos los ángulos en de dos rotaciones,
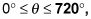
que tiene un seno con ese valor, y los puso igual a
Los otros dos ángulos son sólo 360 más que los dos primeros correspondiente.
Divida los términos en ambos lados de la ecuación por 2 para resolver
Observe cómo todas las soluciones
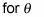
son entre 0 y 360 grados - al igual que preguntas.
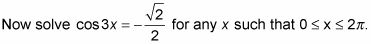
Escribe la ecuación inversa.
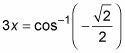
Lista de todos los ángulos en de tres rotaciones,
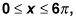
que tienen que coseno, y los puso igual a 3X.
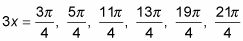
Los otros dos ángulos son sólo
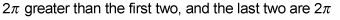
mayor que el segundo dos.
Multiplique ambos lados por un tercio para resolver X.
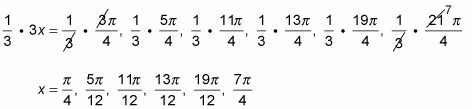
Este resultado muestra la gran ventaja de radianes - los números no obtienen tan grande como lo hacen con grados. La desventaja puede estar teniendo tantas fracciones.
Cómo calcular los ángulos de referencia en grados Despejando el ángulo de referencia en grados es mucho más fácil que tratar de determinar una función trigonométrica del ángulo original. Para calcular la medida (en grados) del ángulo de referencia para cualquier ángulo theta dado, utilizar…
¿Cómo distinguir entre las funciones y las relaciones trigonométricas Técnicamente, se supone que una función trigonométrica inversa de tener sólo una salida para cada entrada. (Parte de la definición de una inversa es que la función inversa y son uno-a-uno.) Con cualquier función uno a uno, cada entrada tiene…
Cómo factorizar expresiones trigonométricas con títulos superiores a 2 Aunque factoring cuadráticas es una brisa, factoring ecuaciones de trigonometría con grados más altos pueden ser un poco desagradable si usted no tiene una situación agradable, como sólo dos términos o una ecuación de segundo grado similar. A…
¿Cómo encontrar una solución a una ecuación trigonométrica de múltiples ángulos Expresiones trigonometría múltiple de ángulo son aquellos en los que la medida del ángulo es algún múltiplo de una variable - por ejemplo, 2X o 3y. Usted puede tomar estas expresiones separadas y despejar todas las soluciones adicionales que…
Cómo localizar ángulos de referencia Cada uno de los ángulos en un círculo unidad tiene un ángulo de referencia, que es siempre un ángulo agudo positivo (excepto los ángulos que ya son positivas y aguda). Al identificar el ángulo de referencia, se puede determinar los valores de…
Cómo cambiar el nombre de los ángulos coterminales Cualquier ángulo puede tener muchas, muchas descripciones en términos de medidas de ángulos, ya que un ángulo es equivalente a sus ángulos coterminales. Las medidas de los ángulos positivos utilizados con mayor frecuencia son los que miden…
¿Cómo resolver una ecuación trigonométrica que tiene múltiples funciones trigonométricas Algunas ecuaciones de trigonometría contienen más de una función trigonométrica. Otros tienen mezclas de múltiples ángulos y ángulos individuales con la misma variable. Algunos ejemplos de tales ecuaciones incluyen 3cos2 X = Sen2 X, 2 seg X =…
Cómo cuadrar ambos lados de una ecuación trigonométrica Cuando la resolución de ecuaciones de trigonometría, más de un método generalmente funciona - a pesar de un método es a menudo más rápido o más fácil que otro. Con la práctica, usted obtendrá buenos en la elección de la mejor de las…
Identificar ángulos coterminales Dos ángulos son coterminal si tienen el mismo lado terminal. Usted tiene un número infinito de formas de dar una medida de ángulo de un rayo terminal en particular. A veces, el uso de un ángulo negativo en lugar de un ángulo positivo es más…
Identificar los dominios y rangos de las funciones trigonométricas inversas Una función que tiene una inversa tiene exactamente una salida (perteneciente a la alcance) Para cada entrada (perteneciente a la dominio), y viceversa. Para mantener las funciones trigonométricas inversas en consonancia con esta definición, hay…
Los ángulos positivos y negativos en un círculo unitario El círculo unidad es una plataforma para la descripción de todas las posibles medidas de los ángulos de 0 a 360 grados, todos los negativos de esos ángulos, además de todos los múltiplos de los ángulos positivos y negativos de menos infinito…
Identidades de producto a suma Las identidades trigonométricas de producto a suma se parecen mucho. Hay que prestar mucha atención a las diferencias sutiles para que pueda aplicarlas correctamente. A pesar de que el producto se ve bonito y compacto, que no siempre es tan fácil…