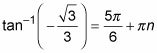¿Cómo distinguir entre las funciones y las relaciones trigonométricas
Técnicamente, se supone que una función trigonométrica inversa de tener sólo una salida para cada entrada. (Parte de la definición de una inversa es que la función inversa y son uno-a-uno.) Con cualquier función uno a uno, cada entrada tiene una salida, y cada salida tiene una entrada.
Para todos los usos prácticos de inversas trigonométricas, tiene una forma de evitar esta regla. Puede designar si desea una respuesta o muchas respuestas utilizando ya sea el inverso función o la inversa relación. Una relación es un poco más flojo que una funcionalidad que permite más de una salida para tener la misma entrada. Para diferenciar entre estas dos entidades, la práctica común es utilizar mayúsculas para las letras de función y minúsculas para la relación.
| Funciones trigonométricas | Relaciones trigonométricas |
|---|---|
| SIN-1 x o Arcsin x | SIN-1 x o arcsin x |
| Cos-1 x o Arccos x | cos-1 x o arccos x |
| Tan-1 x o Arctan x | tan-1 x o x arctan |
| Cuna-1 x o arccot x | cot-1 xo arccot x |
| Sec-1 x o x segundos de arco | seg-1 x o x arcsec |
| Csc-1 x o arccsc x | csc-1 x o arcscs x |
Si se escribe la función
Existe una sola respuesta, que se llama la valor principal de la inversa. Pero si escribes
a continuación, el resultado puede ser de 30 grados, 150 grados, 390 grados, 510 grados, y así sucesivamente
Todo depende de la situación - lo que quiere en el momento. ¿Quieres simplemente el valor principal, o quieres múltiples valores? O puede que quiera un montón de valores dentro de una rotación completa - de 0 a 360 grados.
Cuando quieres un montón y un montón de ángulos o respuestas, enumerando todos ellos puede ser tedioso. De hecho, enumerando todas las soluciones posibles puede incluso no ser factible. En lugar de hacer una lista, usted puede dar un regla, el cual le permite definir un ángulo con todos sus múltiplos de rotación completa - los ángulos con el mismo lado del terminal.
Dejar n representar cualquier número entero (..., -3, -2, -1, 0, 1, 2, 3,...). Usando el n como un multiplicador, se puede escribir una larga lista de ángulos de manera más eficiente. En lugar de decir X = 30, 150, 390, 510, 750, 870,. . . , Dividir la lista en dos grupos: X = 30, 390, 750, 1110-. . .- Y X = 150, 510, 870, 1230-. . . - Y luego usar las dos reglas que siguen:
X = 30 + 360n o X = 150 + 360n
Y luego, en radianes, en lugar de decir
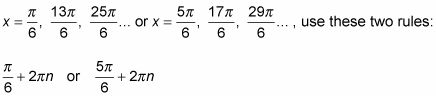
He aquí un ejemplo que muestra cómo escribir todos los ángulos que tienen un coseno igual a
Los pasos implican la resolución de la relación inversa, no sólo encontrar el valor principal para la función. Resuelva para los valores que satisfacen
Enumere varias soluciones, tanto en grados y radianes.

Escriba las respuestas en grados mediante el uso de los dos primeros ángulos más múltiplos de 360.
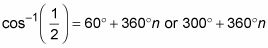
Escriba las respuestas en radianes mediante el uso de los dos primeros ángulos más múltiplos de 2pi-.
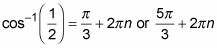
Escribir todos los posibles ángulos de tangente inversa es un poco más fácil que escribir ellos durante seno o coseno. La tangente es positiva en el primer y tercer cuadrantes, que son maliciosa-esquina de uno al otro (media una rotación completa). Debido a este hecho, los ángulos que tienen los mismos valores de la función son 180 grados de separación, y se puede utilizar bonitas múltiplos de 180 grados o pi- para nombrar todas las respuestas. Este no es el caso con seno y el coseno, sin embargo. Los ángulos con los mismos valores de la función son en cuadrantes que son adyacentes entre sí, así que tienes que usar dos reglas separadas - ambos con múltiplos de 360 grados - de nombrar todas las respuestas.
Así es como para escribir todos los ángulos que tienen una tangente igual a
Resolver los valores que satisfacen
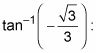
Enumere varias respuestas, tanto en grados y radianes.
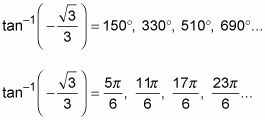
Escriba las respuestas en grados usando múltiplos de 180.
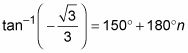
Escriba las respuestas en radianes utilizando múltiplos de pi-.