Exponentes de matemáticas básico común
Estudiantes comunes de matemáticas básicas comienzan a trabajar con exponentes en el octavo grado. En álgebra, que se pueda imaginar exponenciación como multiplicación repetida. La siguiente analogía le ayudará a entender la importancia de esto.
Tu sabes
porque hay 12 cosas en 4 grupos de 3. Si no lo hizo saber el producto
se puede encontrar en varias formas. Usted podría presentar a 4 grupos de 3 cosas y contar uno por uno, por ejemplo. O usted podría utilizar el propiedad asociativa de la multiplicación, lo que significa que para encontrar
usted puede multiplicar la y b primero, o usted puede multiplicar b y c primero - el producto final es la misma en ambos sentidos. Usando la propiedad asociativa, usted podría pensar en
es el doble de lo
Por último, se podría pensar
Es decir, una forma de calcular los productos es mediante el uso de la adición repetida.
Es lo mismo con exponentes:
A partir de 4 y 3, a calcular un tercer número, 64. Así como usted puede calcular
mediante el uso de una suma repetida, puede calcular
utilizando multiplicación repetida:
Pero hay otras formas también, y estas formas dependen de las propiedades de potenciación como una operación. Puede hacer doble
Llegar
utilizando la propiedad asociativa de la multiplicación, y las propiedades de exponenciación permitirá relacionar
Estas propiedades se conocen como reglas para el funcionamiento con exponentes.
Tres reglas principales aparecen en el octavo grado. En las siguientes afirmaciones, A se presume que es un número positivo:
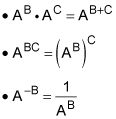
Usted puede entender estas reglas mejor por medio de ejemplos. Usted puede ver la primera regla, que
pensando en
Seis grupos de tres se multiplican. La segunda regla se puede ver por pensar en
Ocho grupos de tres se multiplican entre sí. La tercera regla es la consecuencia lógica de la primera regla, y por el hecho de que
cuando A es cualquier número positivo. He aquí por qué:
por la primera regla. entonces
tiene que ser el recíproco de
Cada una de estas reglas es útil ir en ambas direcciones. Usted no tiene que ver estas ecuaciones como máquinas que transforman la izquierda, lado a la derecha; lado. En cambio, cada lado de cada ecuación tiene el mismo valor que el otro lado. A veces hay algo que se parece a esto:
y es útil para escribir como
A veces se va al revés. Lo que importa es la equivalencia - o igualdad - de ambos lados de cada ecuación.
-
Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 5 -
Multiplique con unidades, pares, y las matrices de matemáticas básico común -
Álgebra: reglas de los exponentes -
Libro de Álgebra para dummies -
Cómo distribuir las variables -
¿Cómo resolver ecuaciones lineales con la multiplicación
Reglas de exponentes Los exponentes son la abreviatura para la multiplicación repetida. Las reglas para las operaciones que involucran exponentes realizar permiten cambiar las expresiones de multiplicación y división con la misma base de algo más simple. Recuerde…
Suma y resta con números negativos El gran secreto para sumar y restar números negativos es convertir a cada problema en una serie de altibajos en la recta numérica. Cuando usted sabe cómo hacer esto, usted encontrará que todos estos problemas son muy simples.No te preocupes por…
Aplicando orden de las operaciones en las expresiones con exponentes Evaluar exponentes de izquierda a derecha antes de de comenzar la evaluación de cuatro grandes operaciones (suma, resta, multiplicación y división). El truco aquí es convertir la expresión en una expresión Big Four y luego usar otro orden…
Básico de matemáticas y pre-álgebra para dummies El sistema de Inglés de las mediciones es más comúnmente utilizado en los Estados Unidos. En contraste, el sistema métrico se utiliza en la mayor parte del resto del mundo. La conversión de las mediciones entre los sistemas métricos Inglés y…
Cómo realizar operaciones asociativas La suma y la multiplicación son tanto operaciones asociativas, lo que significa que puede agrupar de manera diferente sin cambiar el resultado. Esta propiedad de la suma y la multiplicación es también llamado el propiedad asociativa. He aquí un…
Dar sentido a exponentes extraños Los exponentes son una manera rápida para representar la multiplicación repetida. Criar a un base número a la potencia de un exponente significa multiplicando la base por sí mismo el número de veces indicado por el exponente. Por ejemplo:102 =…
Los paréntesis y la propiedad asociativa Paréntesis operaciones del grupo en conjunto, que le dice que hacer ninguna operación dentro de un conjunto de paréntesis antes de usted hace operaciones fuera de ella. Los paréntesis pueden hacer una gran diferencia en el resultado que se…
Los fundamentos de trabajar con exponentes Exponentes (también llamados poderes) son la abreviatura para la multiplicación repetida. Por ejemplo, 23 medios para multiplicar 2 por sí mismo tres veces. Para ello, utilice la siguiente notación:En este ejemplo, 2 es el número base y 3 es el…
¿Cómo resolver una ecuación exponencial con una variable en uno o ambos lados Ya sea una ecuación exponencial contiene una variable en uno o ambos lados, el tipo de ecuación se le pide resolver determina los pasos que se dan para resolverlo.El tipo básico de la ecuación exponencial tiene una variable en un solo lado y se…
La identificación de propiedades algebraicas más utilizados en la resolución de identidades Resolución de identidades es casi un rito de paso para los que estudian trigonometría. Hacer frente a la perspectiva de la resolución de identidades - y más tarde simplificar expresiones trigonométricas en cálculo - va mucho más suavemente si…
ASVAB Preparación: exponentes y notación científica Muchos de los problemas que se ven en las subpruebas de matemáticas ASVAB requieren que usted realice cálculos que involucran exponentes y notación científica. Si esto suena confuso, no preocupe, no es realmente. Siga leyendo.Consejos sobre los…
Preparación ASVAB: examen de álgebra Usted se encontrará con problemas de álgebra en el ASVAB. Problemas de álgebra son ecuaciones, lo que significa que las cantidades a ambos lados del signo igual son iguales - son la misma: 2 = 2, 1 + 1 = 2, y 3 - 1 = 2. En todos estos casos, las…