Cómo utilizar mercados, el conjugado hermitiano y notación bra-ket
¿Qué Dirac notación y el conjugado hermítica tienen en común? Ayudan a los físicos para describir muy, muy grandes vectores. En la mayoría de los problemas de la física cuántica, los vectores pueden ser infinitamente grande - por ejemplo, una partícula en movimiento pueden estar en un número infinito de estados. Manejo de grandes conjuntos de estados no es fácil usando la notación vectorial, así que en vez de escribir explícitamente todo el vector cada vez, la física cuántica generalmente utiliza la notación desarrollada por el físico Paul Dirac - la Dirac o notación bra-ket.
Conteúdo
Abreviando vectores de estado como las TFE
Notación de Dirac abrevia el vector de estado como ket, Me gusta esto:
Por ejemplo, si estuviera tratando de encontrar las probabilidades de lo que era probable que muestran un par de dados laminados, podría escribir el vector de estado como un ket de esta manera:
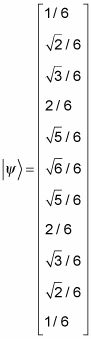
Aquí, los componentes del vector de estado están representadas por números. Más comúnmente, sin embargo, cada componente representa una función, algo como esto:
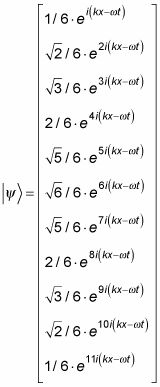
Puede utilizar funciones como componentes de un vector de estado, siempre y cuando sean linealmente funciones independientes (y por lo que se pueden tratar como ejes independientes en el espacio de Hilbert). En general, un conjunto de vectores
en el espacio de Hilbert es linealmente independiente si la única solución a la ecuación siguiente es que todos los coeficientes layo = 0:
Es decir, siempre y cuando no se puede escribir cualquier vector como combinación lineal de los otros, los vectores son linealmente independientes y por lo tanto constituyen una base válida en el espacio de Hilbert.
Escribiendo el conjugado hermítica como un sostén
Por cada cado, hay un sostén correspondiente. (Los términos provienen de bra-ket, o soporte.) LA sostén es el conjugado hermítica del cado correspondiente.
Supongamos que usted comience con esta cado:
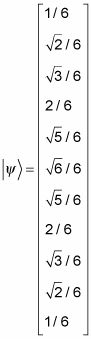
El símbolo asterisco (*) en la siguiente ecuación significa el complejo conjugado. (LA complejo conjugado voltea la señal que conecta las partes real e imaginaria de un número complejo.) De modo que el sujetador correspondiente, que se escribe como
El sujetador es este vector fila:
Tenga en cuenta que si alguno de los elementos del mer- son números complejos, usted tiene que tomar su complejo conjugado al crear el sostén asociado. Por ejemplo, si su número complejo en el ket es la + bi, su complejo conjugado en el sujetador es la - bi.
Multiplicando sujetadores y mercados
Usted puede tomar el producto de su cado y el sujetador, denota como
Me gusta esto:
Esto es sólo la multiplicación de matrices, y el resultado es el mismo que tomar la suma de los cuadrados de los elementos:
Y esa es la manera que debe ser, porque la probabilidad total debe sumar 1. Por lo tanto, en general, el producto del sujetador y ket es igual a 1:
Si esta relación se mantiene, el mer-
se dice que está normalizado.
-
Cómo utilizar el menú CMPLX en la TI-84 Plus -
Matemáticas normas fundamentales comunes: el sistema de números complejos -
Adición y sustracción de vectores -
Los números complejos en pre-cálculo -
Cómo realizar operaciones con números complejos -
Cálculo del vector resultante de dos vectores de desplazamiento
Encuentra las funciones propias de lz en coordenadas esféricas En algún momento, su instructor física cuántica puede pedirle que encontrar las funciones propias de la Lz en coordenadas esféricas. En coordenadas esféricas, la Lz operador tiene este aspecto:que es la siguiente:Y por esoesta ecuación se…
La fuerza es un vector Fuerza, como el desplazamiento, velocidad y aceleración, es una cantidad vectorial, que es la razón por la segunda ley de Newton se escribe como sigmaF = ma. Poner en palabras, se dice que la suma vectorial de las fuerzas que actúan sobre un…
Cómo agregar dependencia del tiempo y obtener una ecuación física para los problemas de partículas libres en tres dimensiones En algún momento, su instructor física cuántica puede querer que usted agregue dependencia del tiempo y obtener una ecuación física para un problema partícula libre en tres dimensiones. Puede agregar dependencia del tiempo de la solución…
Cómo agregar vectores en una cuadrícula Puede utilizar los componentes de vectores para agregar vectores juntos utilizando una cuadrícula. Si lo hace, reduce el problema de la adición de vectores a una simple combinación de la adición de números juntos, lo cual es muy útil cuando a…
Cómo organizar eingenvectors En la física cuántica, los vectores propios de un operador hermítica definen un conjunto completo de vectores ortonormales - es decir, una base completa para el espacio de estados. Cuando se ve en este " base propia, " que se construye de los…
Cómo montar probabilidades relativas en un vector En la física cuántica, las probabilidades toman el lugar de las mediciones absolutas. Digamos que usted ha estado experimentando con rodar un par de dados y están tratando de averiguar la probabilidad relativa de que los dados se mostrarán…
Cómo crear un vector Un vector es una combinación de exactamente dos valores: una magnitud (como la velocidad de un objeto en movimiento) y una dirección (tal como la dirección de un objeto en movimiento). Todo tipo de cosas se pueden describir con vectores,…
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
¿Cómo encontrar el operador adjunto En la física cuántica, a menudo trabaja con adjoints hermitianas. los Operador adjunto - también llamado adjunto o Conjugado hermítica - de un operador A se denotaPara encontrar el operador adjunto, sigue estos pasos:Reemplazar constantes…
¿Cómo encontrar la inversa de una matriz grande Encontrar la inversa de una matriz grande muchas veces no es fácil, por lo que los cálculos de física cuántica a veces se limita a trabajar con operadores unitarios, T, donde inversa del operador es igual a su adjunto,(Para encontrar el adjunto…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
Como restar vectores Usted no viene a través del vector resta muy a menudo en problemas de física, pero sí aparecerá. Para restar dos vectores, que puso sus pies (o colas, las partes no puntiagudos) juntos- entonces dibujar el vector resultante, que es la diferencia…