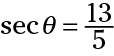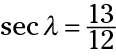Las funciones cosecante y secante
los cosecante función, abreviado csc, es el recíproco de la función seno y por lo tanto utiliza esta relación: hipotenusa / opuesto. La hipotenusa de un triángulo rectángulo es siempre el lado más largo, por lo que el numerador de esta fracción es siempre mayor que el denominador. Como resultado, la función cosecant siempre produce valores más grandes que 1.
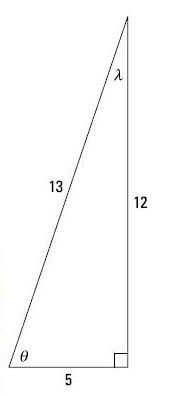
Puede utilizar los valores indicados para determinar los cosecantes de los dos ángulos agudos:
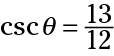
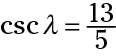
Supongamos que alguien te pide que encontrar la cosecante del ángulo alfa si sabe que la hipotenusa es 1 unidad de largo y que el triángulo rectángulo es isósceles. Recuerde que un triángulo isósceles tiene dos lados congruentes. Estos dos lados tienen que ser las dos patas, porque la hipotenusa tiene que tener el lado más largo. Por lo tanto, para encontrar la cosecante:
Encuentra las longitudes de las dos piernas.
El teorema de Pitágoras dice que la2 + b2 = c2, pero debido a que dos lados son congruentes, puedes sacar una variable y escribir la ecuación como la2 + la2 = c2. Ponga en 1 para el c y resuelve para la.
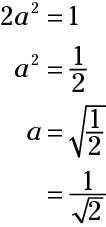
Las patas son tanto
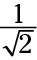
unidades de largo. Puede dejar el radical en el denominador y no preocuparse por la racionalización, porque vas a la entrada de todo el asunto en la relación cosecante, de todos modos, y las cosas pueden cambiar.
Utilice la longitud del lado opuesto en la relación para cosecant.
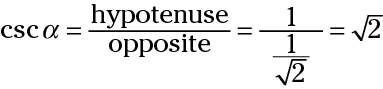
los secante función, abreviado seg, es el recíproco del coseno. Por lo tanto, su relación es hipotenusa / adyacente. Al igual que con la cosecante, la relación de los lados es mayor que 1. Utilizando el triángulo en la figura, los dos secantes se
-
Matemáticas normas fundamentales comunes: similitud, triángulos rectángulos, y trigonometría -
¿Cómo medir los triángulos -
Cómo calcular un ángulo usando funciones trigonométricas recíprocas -
Cómo calcular los valores para las seis funciones trigonométricas -
Cómo graficar una función cosecante -
Cómo utilizar SOHCAHTOA para encontrar las funciones trigonométricas de un triángulo rectángulo
¿Cómo trabajar con triángulos 30-60-90 grados Todos los triángulos 30-60-90 grado tienen lados con la misma relación básica. Si nos fijamos en el triángulo 30-60-90 grados en radianes, que se traduce en lo siguiente:En cualquier 30-60-90 triángulo, vea el siguiente:La pierna más corta…
Aplicando el teorema de Pitágoras El teorema de Pitágoras se ha conocido durante al menos 2.500 años. Se utiliza el teorema de Pitágoras cuando se sabe las longitudes de dos lados de un triángulo rectángulo y quiere averiguar la longitud del tercer lado.El teorema de…
La clasificación de tres tipos de triángulos Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos. Es decir, un triángulo tiene tres lados, y tres términos…
Problemas de la práctica de la geometría con triángulos y polígonos LA polígono es una figura geométrica que tiene al menos tres lados. El triángulo es el polígono más básico. Usted encontrará las siguientes fórmulas y propiedades útiles al responder a las preguntas que implican desigualdades triángulo,…
Identificar escaleno, isósceles y triángulos equiláteros Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos.Las siguientes son las clasificaciones de triángulos basada en…
La identificación de la 45 - triángulo de 90 grados - 45 Un 45 a 45 - 90 grados triángulo (o triángulo rectángulo isósceles) es un triángulo con ángulos de 45 # 176-, 176- 45 # y 90 # 176- y los lados de la relación entreTenga en cuenta que se trata de la forma de la mitad de un cuadrado, corte a…
La identificación de triángulos por sus ángulos Se puede clasificar triángulos por sus ángulos, así como por sus lados. Las clasificaciones basadas en ángulos son como sigue:Triángulo aguda: Un triángulo con tres ángulos agudos (menos de 90 # 176-).Triángulo obtuso: Un triángulo con un…
La determinación de si un objeto largo encaja en una esquina pasillo Aquí hay una aplicación de la trigonometría que puede muy bien ser capaz de relacionarse con: ¿Alguna vez ha tratado de conseguir un mueble grande en una esquina en una casa? Usted girar y girar y lo puso de punta, pero fue en vano. En este…
Dominios y rangos de funciones trigonométricas El dominio de una función se compone de todos los valores de entrada que una función puede manejar - la manera que la función está definida. Por supuesto, usted desea conseguir valores de salida (que conforman la gama) cuando introduce valores…
Funciones trigonométricas secantes gama de Dominio y cosecante y Las funciones cosecante y secante están estrechamente ligados a seno y coseno, porque son los respectivos recíprocos. En referencia al plano de coordenadas, cosecante es r/y, y secante es r/X. El valor de r es la longitud de la hipotenusa de un…
Sine Express en términos de secante o cosecante A pesar de que cada función trigonométrica es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener algunos…
Grafica la función cosecante Una manera muy eficaz de graficar la función cosecante es hacer primero un boceto rápido de la función seno (su recíproco). Con el boceto de seno en su lugar, se puede dibujar las asíntotas de la función cosecante a través de la X-intercepta…