Cómo calcular un intervalo de confianza del 95 por ciento

categoría Las pequeñas empresas y carreras / El funcionamiento de su negocio / Planificación estratégica

Para calcular un intervalo de confianza del 95%, que necesita tres datos: la media (para los datos continuos) o proporción (para datos binarios) - la desviación estándar, que describe cómo dispersa los datos están alrededor de la media- y el tamaño de la muestra.

Ejemplo datos continuos

Imagínese que usted pidió 50 clientes qué tan satisfechos estaban con su reciente experiencia con el producto en una escala de 7 puntos, con 1 = Nada satisfecho y 7 = extremadamente satisfecho. Estos son los pasos que debe seguir para calcular un intervalo de confianza alrededor de su promedio de la muestra:

  1. Encuentre la media sumando las puntuaciones de cada uno de los 50 clientes y se divide por el número total de respuestas (que es 50).

    Si tiene Microsoft Excel, puede utilizar la función = PROMEDIO () para este paso. A los efectos de este ejemplo, usted tiene una respuesta promedio de 6.

  2. Calcular la desviación estándar.

    Puede utilizar la fórmula de Excel =STDEV () para todos los 50 valores. Usted tiene una desviación estándar de la muestra de 1,2.

  3. Calcular el error estándar dividiendo la desviación estándar por la raíz cuadrada del tamaño de la muestra.

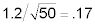
    image0.jpg

  4. Calcule el margen de error multiplicando el error estándar por 2.

    .17 x 2 = 0,34

  5. Calcule el intervalo de confianza al añadir el margen de error a la media de la etapa 1 y luego restando el margen de error de la media, así:

    6 + 0,34 = 6,34

    6 - 0.34 = 5.66

    Ahora sabe que tiene un intervalo de confianza del 95% de 5,66 a 6,34. La mejor estimación de lo que la satisfacción del promedio de toda la población al cliente es oscila entre 5,66 y 6,34.

Si usted tiene una muestra más pequeña, es necesario utilizar un múltiplo mayor que 2. Usted puede encontrar lo múltiple que necesita con una calculadora en línea.

Ejemplo de datos discretos

Imagínese que usted pidió 50 clientes si van a recomprar su servicio en el futuro. Usando una variable ficticia, puede codificar Sí = 1 y n = 0. Si 40 de 50 reportan su intención de recompra, puede utilizar lo que se llama la técnica de Wald ajustado para encontrar su intervalo de confianza:

  1. Encuentra el promedio sumando todos los 1s y dividiendo por el número de respuestas.

    40/50 = 0,8

  2. Ajuste la proporción para que sea más precisa.

  1. Añadir 2 para el numerador (el número de 1s).

    40 + 2 = 42

  2. Encuentre el tamaño de la muestra ajustado añadiendo 4 al denominador (total de las respuestas).

    50 + 4 = 54

  3. Divida el resultado de encontrar la proporción ajustada.

    42/54 = 0,78

  • Calcule el error estándar para los datos de proporción.

    1. Multiplicar la proporción ajustada por 1 menos la proporción ajustada.

      .78 x (1 - 0,78). = 17

    2. Divida el resultado (0.17) por el tamaño de la muestra ajustada desde el paso 2.

      .17/54 = 0,0031

    3. Determinar la raíz cuadrada del valor de la etapa anterior.

      image1.jpg

    4. Calcule el margen de error multiplicando el error estándar (resultado del paso 3) por 2.

      .057 x 2 = 0,11

    5. Calcule el intervalo de confianza añadiendo el margen de error de la proporción de la Etapa 1 y restando el margen de error de la proporción.

      .78 + 0,11 = 0,89

      .78 - ,11 = 0,67

      El intervalo de confianza del 95% es 0,67-0,89. La mejor estimación de la intención de toda la población de clientes de recompra es de entre 67% y 89%.

      6. Los valores se redondean en los pasos anteriores para mantenerlos simple. Si quieres un intervalo de confianza más preciso, utilice la calculadora en línea.



      Artículos Relacionados

      Sobre el autor
      Cómo calcular un intervalo de confianza para una media poblacional cuando se conoce la desviación estándar Cómo calcular un intervalo de confianza para una media poblacional cuando se conoce la desviación estándar

      Si conoce la desviación estándar de una población, entonces se puede calcular un intervalo de confianza (IC) para la media o promedio, de esa población. Cuando una característica estadística que está siendo medido (tales como ingresos, IQ,…

      Cómo calcular un intervalo de confianza para una media poblacional con una desviación estándar desconocida y / o pequeño tamaño de la muestra Cómo calcular un intervalo de confianza para una media poblacional con una desviación estándar desconocida y / o pequeño tamaño de la muestra

      Usted puede calcular un intervalo de confianza (IC) para la media o promedio, de una población, incluso si la desviación estándar es desconocida o el tamaño de la muestra es pequeño. Cuando una característica estadística que está siendo…

      Cómo calcular el margen de error para una media muestral Cómo calcular el margen de error para una media muestral

      Cuando una pregunta de investigación pide a encontrar una estadística media de la muestra (o promedio), es necesario reportar un margen de error, o el Ministerio de Educación, para la media de la muestra. La fórmula general para el margen de…

      Cómo calcular el margen de error para una proporción de la muestra Cómo calcular el margen de error para una proporción de la muestra

      Al informar los resultados de una encuesta estadística, es necesario incluir el margen de error. La fórmula general para el margen de error para una proporción de la muestra (si se cumplen ciertas condiciones) esdóndees la proporción de la…

      Cómo determinar el tamaño mínimo necesario para una muestra estadística Cómo determinar el tamaño mínimo necesario para una muestra estadística

      El margen de error de un intervalo de confianza (IC) se ve afectada por las dimensiones de la muestra- estadística como el tamaño aumenta, margen de error disminuye. En cuanto a esta a la inversa, si quieres un menor margen de error (y no lo hace…

      Cómo determinar el intervalo de confianza para una proporción de la población Cómo determinar el intervalo de confianza para una proporción de la población

      Usted puede encontrar el intervalo de confianza (IC) para una proporción de la población para mostrar la probabilidad estadística de que es probable que se produzcan dentro de la población de una característica.Cuando una característica que se…

      ¿Cómo encontrar t *-valores para los intervalos de confianza ¿Cómo encontrar t *-valores para los intervalos de confianza

      Intervalos de confianza estimación de los parámetros de población, tales como la media poblacional, mediante el uso de una estadística (por ejemplo, la media de la muestra) más o menos un margen de error. Para calcular el margen de error para…

      Vinculación de margen de error y la población proporción Vinculación de margen de error y la población proporción

      Las preguntas de práctica aquí tienen que trabajar en el margen de error para los medios de la población y proporciones poblacionales. Resolver los siguientes problemas relacionados con el margen de error y la población proporción.La tabla…

      Estadísticamente calcular tamaño de la muestra Estadísticamente calcular tamaño de la muestra

      En el diseño de un estudio, el tamaño de la muestra es una consideración importante, ya que cuanto mayor sea el tamaño de la muestra, más datos que usted tiene, y cuanto más precisos serán los resultados (suponiendo datos de alta calidad). Si…

      Estadísticas para los maniquíes Estadísticas para los maniquíes

      Después que los datos se han recogido, el primer paso en el análisis es a crujir algunas estadísticas descriptivas para hacerse una idea de los datos. Por ejemplo:¿Dónde está el centro de datos ubicado?Cómo extendido son los datos?Cómo…

      Topografía intervalos de confianza estadísticos Topografía intervalos de confianza estadísticos

      En estadística, un intervalo de confianza es una conjetura acerca de algunas características de la población. Un intervalo de confianza contiene un plus estimación o menos un inicial margen de error (la cantidad que usted espera que sus…

      El intervalo de confianza en torno a una media El intervalo de confianza en torno a una media

      Del mismo modo que la SE fórmulas (error estándar) dependen de qué tipo de estadística de la muestra que está tratando con (ya sea que estés medir o contar algo o conseguir que a partir de un programa de regresión o de algún otro cálculo),…

      » » » » Cómo calcular un intervalo de confianza del 95 por ciento