Un dolor de cabeza común tarea central: restando añadiendo
Un cambio importante en los estándares de matemáticas básicas comunes es que los estudiantes deben trabajar a través de los cálculos de varios dígitos por pensar en relaciones numéricas antes de que se espera que sigan algoritmos estándar. Para los padres que nunca tuvieron que pensar en sus cálculos en la escuela, esto puede hacer que el tiempo la tarea un poco intimidante.
Por ejemplo, un método de sustracción como éste fue en torno a Internet, con la gente que expresa horror por lo complicado que el básico común hace que la aritmética simple.
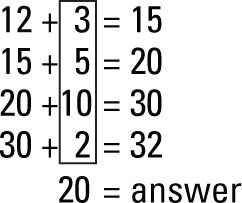
En la superficie, este problema sin duda tiene un aspecto complicado. ¿De dónde viene el 3 viene? ¿Qué significa 15 tienen que ver con restar 12 del 32? ¿Por qué no hacerlo de la manera pasada de moda?
Si usted cava un poco más profundo, se puede ver que estas buenas preguntas tienen respuestas razonables. Los niños aprenden a contar por decenas y cinco años en el jardín de infantes y primer grado, lo que significa que son múltiplos de cinco puntos de referencia familiares en el sistema numérico. El 3 no hace mágicamente apariencias sino que es lo que necesita para llegar a 15, un múltiplo de cinco. Entonces usted puede contar de cinco en cinco.
Algunos niños pueden utilizar el mismo tipo de pensamiento y utilizar 8 como su primer número, que es lo que necesita para obtener de 12 a 20. Adición de 8 a 12 inmediato es otro caso de utilizar un hecho memorizado estratégicamente. (Aquí el hecho relacionado es que 2 + 8 = 10, por lo que 12 + 8 = 20.) Después de que el estudiante está en 20, que es otra de 10 a 30, y, finalmente, dos más para llegar a 32. Otros niños pueden notar que el 32 y 12 tienen el mismo dígito de las unidades, por lo que puede contar con 12, 22, 32 - de dos pasos de diez.
No se debe confundir el hecho de que múltiples estrategias se discuten en clase para un mandato de que todos los estudiantes dominen todas estas estrategias. Los maestros no están tratando de aumentar el número de cosas que los estudiantes necesitan para recordar. Más bien, están exponiendo a los estudiantes a una serie de formas correctas de pensar para que los estudiantes puedan reconocer y construir sobre sus propias ideas.
El punto de este tipo de trabajo es ayudar a los niños a desarrollar la suma y la resta como operaciones relacionadas, no conjuntos separados de hechos que hay que aprender. La comprensión de las relaciones entre los hechos reduce el número de errores de los estudiantes a hacer, el tamaño de los errores que hacer hacer, y su dependencia de las calculadoras en el largo plazo.
-
Clase de la ciencia y el microscopio ipad móvil ProScope -
4 maneras de que los estándares básicos comunes ayudan a los estudiantes a aprender matemáticas - Matemáticas básico común para los padres para los maniquíes
- Matemáticas básico común para los padres: haciendo preguntas en tiempo de la tarea
- Normas básicas comunes para las matemáticas
- Fundamentos Estándares Básicos Comunes
Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 1 En Grado 1, por las normas fundamentales comunes, los estudiantes expanden sus habilidades con los números e incorporar el uso de más números y detalles en la resolución de problemas de matemáticas y mirando a las formas. Estándares Básicos…
Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 2 En grado 2, por las normas fundamentales comunes, los estudiantes comienzan a construir una base conceptual para la multiplicación como piensan en la combinación de los grupos al agregar. Los estudiantes siguen encontrando más compleja…
Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 5 En 5to grado, los estudiantes se encuentran con nuevos componentes en los problemas de matemáticas para las normas fundamentales comunes, tales como soportes y paréntesis. Ciertos conceptos introducidos en grados anteriores, tales como el trabajo…
Las normas fundamentales comunes: los estándares de contenido de matemáticas de dominio Los estándares de contenido básicos comunes para las matemáticas son parte de los dominios específicos, o categorías, que a menudo son relevantes a niveles múltiples de grado. La idea detrás de este enfoque es que ciertos conceptos en curso…
Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el jardín de infantes Hay ciertos conceptos matemáticos que un niño va a encontrar en cada grado que se presta a su capacidad para satisfacer las normas fundamentales comunes. En el jardín de infantes, las matemáticas se centra en dos áreas:Los números enteros: Los…
Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 3 La multiplicación, división y fracciones son componentes clave de las habilidades y conceptos estudiantes encuentran a las normas fundamentales comunes en el grado 3. Los estudiantes también continúan trabajando con las formas. Estándares…
Diferenciar entre gcfs y lcms en matemáticas núcleo común En Common Core matemáticas, estudiantes de sexto grado aplican su conocimiento de los factores y los múltiplos de buscar el máximo común divisor (o GCF) de dos números y el mínimo común múltiplo (mcm) de dos números.los máximo común…
Cómo descomponer números de ayuda a los estudiantes con las matemáticas núcleo común En Common Core matemáticas, los estudiantes de primer grado tienen que empezar a pensar en las propiedades de los números más profundamente. Una propiedad importante de todos los números es que se pueden descomponer.Cuando tú descomponer un…
¿Cómo los estudiantes aprenden sobre la medición en matemáticas núcleo común En segundo grado de matemáticas, los estudiantes Common Core utilizan reglas para medir longitudes. Al hacer esto, se están conectando y extender el uso de unidades no estándares tales como clips de papel y cubos de unión, que aprendieron acerca…
Cómo reducir la frustración con la tarea de matemáticas básico común Sea cual sea matemáticas estándares pueden ser - Common Core o cualquier otra cosa - la mayoría de los niños estarán frustrados con una tarea de vez en cuando. El consejo para usted, el padre, no cambia sólo porque su estado natal ha adoptado…
Mantenga hechos básicos comunes de matemáticas rectas Una gran cantidad de información errónea es disponible de las normas fundamentales comunes. Estas normas guían las matemáticas su niño aprende en la escuela cada año. Con el fin de promover y apoyar a su hijo, usted necesita estar bien…
Formas de partición para hacer fracciones unitarias en matemáticas núcleo común Core cosas comunes partición estudiantes de matemáticas de tercer grado, y que nombran las piezas resultantes utilizando fracciones. Particiones en este contexto significa esquejes cosas en trozos de igual tamaño.Los niños tienen mucha práctica…