Trabajar con tres dimensiones potenciales rectangulares
Este artículo echa un vistazo a un potencial 3D que forma una caja, como se ve en la siguiente figura. Quiere recibir las funciones de onda y los niveles de energía aquí.
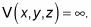
Dentro de la caja, decir que V (X, y, z) = 0, y el borde del área, decir que
Así que tienes lo siguiente:
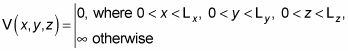
Dividiendo V (X, y, z) En VX(X), Vy(y), Y Vz(z) te dio
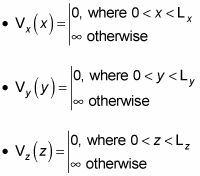
Está bien, porque el potencial tiende a infinito en las paredes de la caja, la función de onda,
debe ir a cero en las paredes, por lo que es su restricción. En 3D, el Schr # 246-dinger ecuación tiene este aspecto en tres dimensiones:
Escribiendo esto le da lo siguiente:
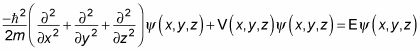
Tome esta dimensión por dimensión. Debido a que el potencial es separable, puede escribir
Dentro de la caja, el potencial es igual a cero, por lo que el Schr # 246-dinger ecuación tiene este aspecto para X, y, y z:
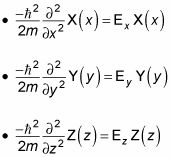
El siguiente paso es volver a escribir estas ecuaciones en términos del número de onda, k. Porque
usted puede escribir las ecuaciones Schr # 246-Dinger para X, y, y z como las siguientes ecuaciones:
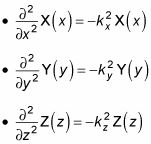
Empieza por tomar un vistazo a la ecuación para X. Ahora usted tiene algo con qué trabajar - una ecuación diferencial de segundo orden,
Estas son las dos soluciones independientes a esta ecuación, donde A y B son aún por determinar:
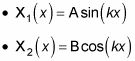
Así que la solución general de
es la suma de las dos últimas ecuaciones:
-
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
Combinar las soluciones para pequeñas y grandes r r en el schr & # 246-dinger ecuación -
La determinación de la parte radial de una función de onda -
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno -
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo -
Cómo partículas pasan a través de las barreras potenciales que tienen menos energía
¿Cómo aplicar el hamiltoniano de un átomo de múltiples electrones neutro Un átomo de múltiples electrones es el sistema de múltiples partículas más frecuente que la física cuántica considera. Se puede aplicar una función de onda de Hamilton a un átomo de múltiples electrones neutro, como se muestra en la…
Cómo desvincular diferentes partículas en ecuaciones linealmente independientes En la física cuántica, se puede desacoplar los sistemas de partículas que se pueden distinguir - es decir, sistemas de identificablemente diferentes partículas - en ecuaciones linealmente independientes. Para ilustrar esto, suponga que tiene un…
Cómo obtener la ecuación 246-dinger schr & # En la física cuántica, la Schr # 246-técnica dinger, que implica la mecánica ondulatoria, utiliza funciones de onda, la mayoría en la base de posición, para reducir las preguntas de la física cuántica a una ecuación diferencial.Werner…
Cómo calcular la ubicación de una partícula aplicando schr & # ecuación de 246-dinger a un paquete de ondas Si usted tiene un número de soluciones a la Schr # 246-dinger ecuación, cualquier combinación lineal de estas soluciones es también una solución. Así que esa es la clave para conseguir una partícula física: Usted agrega varias funciones de…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
Cómo normalizar la función de onda en un potencial cuadro En el curso de física cuántica, se le puede pedir a normalizar la función de onda en un potencial cuadro. He aquí un ejemplo: considere la función de ondaen el X dimensión, tiene esto para la ecuación de onda:Así que la función de onda es…
Cómo simplificar y dividir la ecuación 246-dinger schr & # hidrógeno En la física cuántica, es posible que necesite para simplificar y dividir la Schr # 246-dinger ecuación de hidrógeno. Aquí está la Schr # 246-dinger ecuación mecánica cuántica habitual para el átomo de hidrógeno:El problema es que usted…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
La física cuántica para los maniquíes Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…
Libro de física cuántica para dummies El Schr # 246-dinger ecuación es una de las fórmulas más elementales de la física cuántica. Con la Schr # 246-dinger ecuación, puede resolver para las funciones de onda de las partículas, y que le permite decir todo lo que pueda acerca de la…
Resolución de la función de onda de r utilizando la schr & # ecuación 246-dinger Si su instructor de la física cuántica le pide que resuelva para la función de onda del centro de masas del sistema de electrones / protones en un átomo de hidrógeno, puede hacerlo a través de un Schr # 246-dinger ecuación modificada:Lo que…