Trabajar con tres dimensiones osciladores armónicos
En la física cuántica, cuando se está trabajando en una dimensión, la partícula en general oscilador armónico se parece a la figura que se muestra aquí, donde la partícula se encuentra bajo la influencia de una fuerza de recuperación - en este ejemplo, se muestra como un resorte.
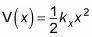
La fuerza de recuperación tiene la forma FX = -kXX en una dimensión, donde kX es la constante de proporcionalidad entre la fuerza sobre la partícula y la ubicación de la partícula. La energía potencial de la partícula como una función de la ubicación X es
Esto también es a veces escrito como
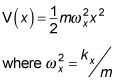
Ahora echa un vistazo al oscilador armónico en tres dimensiones. En tres dimensiones, el potencial se ve así:
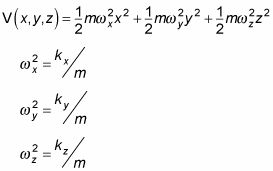
Ahora que tiene un formulario para el potencial, se puede empezar a hablar en términos de la ecuación Schr # 246-dinger:
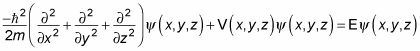
Sustituyendo en el potencial en tres dimensiones, V (x, y, z), Le da esta ecuación:
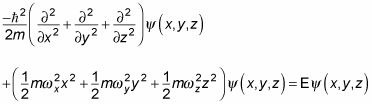
Tome esta dimensión por dimensión. Porque se puede separar el potencial en tres dimensiones, se puede escribir
Por lo tanto, la Schr # 246-dinger ecuación tiene este aspecto para X:
Resolviendo esta ecuación, se obtiene la siguiente solución:
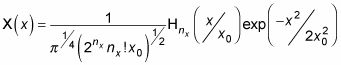
dónde
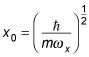
y nX = 0, 1, 2, y así sucesivamente. El HnX término indica un polinomio de Hermite, que se ve así:
H0(X) = 1
H1(X) = 2X
H2(X) = 4X2 - 2
H3(X) = 8X3 - 12X
H4(X) = 16X4 - 48X2 + 12
H5(X) = 32X5 - 160X3 + 120X
Por lo tanto, se puede escribir la función de onda como esto:
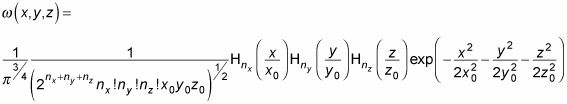
Esa es una forma relativamente fácil para una función de onda, y todo es posible gracias al hecho de que se puede separar el potencial en tres dimensiones.
¿Qué pasa con la energía del oscilador armónico? La energía de un oscilador armónico unidimensional es
Y, por analogía, la energía de un oscilador armónico tridimensional está dada por
Tenga en cuenta que si usted tiene un oscilador armónico isótropo, donde
la energía se ve así:
En cuanto al potencial cúbico, la energía de un oscilador armónico isotrópica 3D es degenerada. Por ejemplo, E112 = E121 = E211. De hecho, es posible tener más de degeneración triple para un oscilador armónico isotrópica 3D - por ejemplo, E200 = E020 = E002 = E110 = E101 = E011.
En general, la degeneración de un oscilador armónico es isotrópica 3D
dónde n = nX + ny + nz.
-
Aplicando la ecuación schr & # 246-dinger en tres dimensiones -
La determinación de la parte angular de una función de onda -
La determinación de la parte radial de una función de onda -
Encontrar la ecuación de energía total para los problemas de partículas libres en tres dimensiones -
Encontrar el schr & # 246-dinger ecuación para el átomo de hidrógeno -
Encontrar la función de onda de una partícula en un cuadrado infinito bien con el tiempo
Cómo determinar estados propios osciladores armónicos de un sistema En la física cuántica, cuando tienes los estados propios de un sistema, se puede determinar los estados permitidos de sistema y la probabilidad relativa de que el sistema estará en cualquiera de esos estados.El conmutador de los operadores A, B…
¿Cómo encontrar cualquier estado excitado de un oscilador armónico Si puede determinar la función de onda para el estado fundamental de un oscilador armónico cuántico, entonces usted puede encontrar cualquier estado excitado de ese oscilador armónico.Por lo tanto, si usted sabe lo queparece, se puede determinar…
¿Cómo encontrar una ecuación de la función de onda en una plaza así infinito Plaza Infinito así, en el que las paredes van al infinito, es un problema de favorito en la física cuántica. Para resolver la función de onda de una partícula atrapada en un pozo cuadrado infinito, sólo tiene que resolver el Schr # 246-dinger…
¿Cómo encontrar el nivel de energía de un oscilador armónico: un ejemplo Su instructor física cuántica puede pedirle que encontrar el nivel de energía de un oscilador armónico. La mejor manera de aprender es a través de un ejemplo. Digamos que usted tiene un protón someterse oscilación armónica concomo se muestra…
¿Cómo encontrar la energía de un oscilador cargada utilizando la teoría de la perturbación En la física cuántica, cuando se tiene los valores propios exactas para un oscilador cargada en un sistema perturbado, puede encontrar la energía del sistema. Basado en la teoría de la perturbación, la energía corregida del oscilador está…
¿Cómo encontrar el estado propio de energía de un oscilador armónico en el espacio posición En la física cuántica, puede utilizar los operadores para determinar el estado propio de energía de un oscilador armónico en el espacio posición. El encanto de la utilización de los operadores la yes que, dado el estado de la tierra, | 0>, los…
¿Cómo encontrar la función de onda del estado fundamental de un oscilador cuántico En la física cuántica, se encuentra la función de onda del estado fundamental de un oscilador cuántico, como la que se muestra en la figura, que toma la forma de una curva de Gauss.El estado fundamental de un oscilador armónico mecánica…
¿Cómo resolver la ecuación 246-dinger schr & # para partículas libres Hay un montón de partículas libres - partículas fuera de cualquier plaza así -en el universo, y la física cuántica tiene algo que decir sobre ellos. El debate se inicia con la Schr # 246-dinger ecuación:Digamos que usted está tratando con…
Cómo utilizar los operadores de creación y aniquilación de resolver problemas oscilador armónico Creación y aniquilación pueden sonar como grandes tipos make-or-break-del-universo de ideas, pero jugar un papel protagonista en el mundo cuántico cuando se trabaja con osciladores armónicos. Utiliza los operadores de creación y aniquilación…
¿Cómo trabajar con un potencial cúbico En la física cuántica, cuando se trabaja con un potencial de caja, usted puede hacer las cosas más simples suponiendo que el cuadro es en realidad un cubo. En otras palabras, L = LX = Ly = Lz. Cuando el cuadro es un cubo, la ecuación de la…
La medición de la energía de las partículas consolidadas y no consolidadas En la física cuántica, puede resolver para los estados de energía permitidos de una partícula, ya que está obligado, o atrapado, en un pozo de potencial o no está consolidado, tener la energía para escapar.Echa un vistazo a el potencial en la…
La física cuántica para los maniquíes Uno de los problemas centrales de la mecánica cuántica es calcular los niveles de energía de un sistema. El operador de la energía, llamada Hamiltoniano, abreviado H, le da la energía total. Encontrar a los niveles de energía de un sistema se…