Sustituyendo con expresiones de la forma f (x) multiplicada por h (g (x))
Cuando g'(X) = F(X), Puede utilizar la sustitución u = g(X) Para integrar expresiones de la forma F(X) multiplicada por h(g(X)), Siempre que h es una función que usted ya sabe cómo integrar.
Sustitución de variables ayuda a llenar el vacío dejado por la ausencia de una regla del producto y una regla de la cadena para la integración.
He aquí un peludo mirando integral que realmente responde bien a la sustitución:
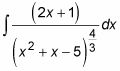
La idea clave aquí es que el numerador de esta fracción es la derivada de la función interna en el denominador. Mira cómo funciona este sistema en esta substitución:
Declarar u igual a la función interna en el denominador y crea la sustitución:
Aquí está la sustitución:
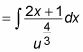
Diferencial du = (2X + 1) dx:
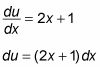
La segunda parte de la sustitución ahora se convierte en claro:
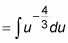
Observe cómo esta sustitución depende de el hecho de que el numerador es la derivada de la función interna en el denominador. (Usted puede pensar que esto es una coincidencia, pero las coincidencias como éstas sucede todo el tiempo en los exámenes!)
La integración es ahora muy sencillo:
Usted toma un paso adicional para eliminar la fracción antes de integrar:
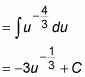
Sustituya la espalda X2 + X - 5 de u:
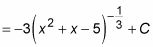
Comprobación de la respuesta mediante la diferenciación con la regla de la cadena revela cómo este problema se creó en el primer lugar:
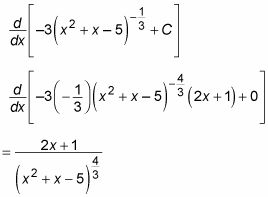
Aquí hay otro ejemplo en el que usted hace una sustitución de variables:
Observe que la derivada de X4 - 1 es X3, off por un factor constante. Así que aquí está la declaración, seguida de la diferenciación:
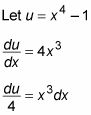
Ahora usted puede hacer las dos sustituciones a la vez:
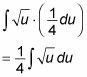
En este punto, puede resolver la integral simple.
Del mismo modo, aquí está otro ejemplo:
A primera vista, esta integral se ve simplemente horrible. Pero en una inspección más detallada, observe que la derivada de cuna X es -csc2 X, así que esto parece otro buen candidato:
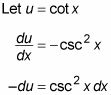
Esto se traduce en la siguiente sustitución:
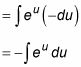
Una vez más, este es otro integrante que pueda solucionar.
¿Cómo integrar expresiones racionales utilizando la suma, constante múltiple, y las reglas de alimentación En muchos casos, puede desenredar expresiones racionales peludas e integrarlos utilizando las reglas anti-diferenciación más la regla de la suma, la Regla múltiplo constante, y la Regla de energía.La regla de la suma para la integración le dice…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
¿Cómo resolver los límites de factoring Usted puede utilizar la técnica algebraica de factoring para resolver " verdadero " problemas de límite. Todos los métodos algebraicos implican la misma idea básica. Cuando la sustitución no funciona en la función original - por lo general a…
¿Cómo resolver los límites de la multiplicación conjugada Para resolver ciertos problemas de límite, tendrá la técnica de multiplicación conjugado. Cuando la sustitución no funciona en la función original - por lo general a causa de un agujero en la función - se puede usar la multiplicación…
¿Cómo resolver límites con álgebra básica Cuando la sustitución no funciona en la función de límite inicial - por lo general a causa de un agujero en la función - a menudo se puede usar un poco de álgebra para manipular la función hasta la sustitución funciona (funciona porque su…
Cómo utilizar l'h & # regla del 244-pital para resolver problemas de límite Regla de L'H # de 244-pital es un gran atajo para hacer algunos problemas de límite. (Y es posible que se necesite algún día para resolver algunos problemas integrales impropias, y también para algunos problemas de series infinitas.)Al igual que…
Integrar una función utilizando el caso sine Cuando la función está integrando incluye un término de la forma (la2 - bx2)n, llamar su triángulo sustitución trigonométrica para el caso sinusoidal. Por ejemplo, supongamos que desea evaluar la siguiente integral:Este es un caso sinusoidal,…
Integrar una función utilizando el caso tangente Cuando la función está integrando incluye un término de la forma (la2 + X2)n, llamar su trigonometría triángulo de sustitución para el caso tangente. Por ejemplo, supongamos que desea evaluar la siguiente integral:Este es un caso tangente,…
Saber cuando para evitar la sustitución de la trigonometría Es útil saber cuándo debe evitar el uso de la sustitución trigonométrica. Con algunas integrales, es mejor ampliar el problema en un polinomio. Por ejemplo, mira la siguiente integral:Esto puede parecer un buen lugar para utilizar la…
Saber cuándo integrar por partes Es importante reconocer que la integración por partes es útil. Para empezar, aquí hay dos casos importantes cuando la integración por partes es definitivamente el camino a seguir:La función logarítmica ln XLas cuatro primeras funciones…
La creación de fracciones parciales cuando se tiene factores lineales distintos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. El caso más simple en el que las fracciones parciales son útiles es cuando el denominador…
La creación de fracciones parciales cuando se ha repetido factores cuadráticos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores cuadráticos…